Trên mặt nước tại hai điểm S1, S2 người ta đặt hai nguồn sóng cơ kết hợp, dao động điều hoà theo phương thẳng đứng với phương trình uA = 6cos40πt và uB = 8cos(40πt) (uA và uB tính bằng mm, t tính bằng s). Biết tốc độ truyền sóng trên mặt nước là 40cm/s, coi biên độ sóng không đổi khi truyền đi. Trên đoạn thẳng S1S2, điểm dao động với biên độ 1cm và cách trung điểm của đoạn S1S2 một đoạn gần nhất là:
Trả lời bởi giáo viên
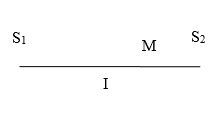
Cách 1: Bước sóng l = v/f = 2 cm., I là trung điểm của S1S2
Xét điểm M trên S1S2: IM = d
\({u_{{S_{1M}}}} = 6cos(40\pi t - \dfrac{{2\pi (\dfrac{{{S_1}{S_2}}}{2} + d)}}{\lambda }) = 6cos(40\pi t - \pi d - \dfrac{{{S_1}{S_2}}}{2}\pi ){\rm{ }}mm\)
\({u_{{S_{2M}}}} = 8cos(40\pi t - \dfrac{{2\pi (\dfrac{{{S_1}{S_2}}}{2} - d)}}{\lambda }) = 8cos(40\pi t + \dfrac{{2\pi d}}{\lambda } - \dfrac{{8\pi }}{\lambda }){\text{ }}mm = 8cos(40\pi t + \pi d - \dfrac{{{S_1}{S_2}}}{2}\pi ){\text{ }}mm.\)
- Điểm M dao động với biên độ 1 cm = 10 mm khi uS1M và uS2M vuông pha với nhau:
\(2\pi d = \dfrac{\pi }{2} + k\pi = > d = \frac{1}{4} + \dfrac{k}{2}\)
d = dmin khi k = 0 => dmin = 0,25 cm .
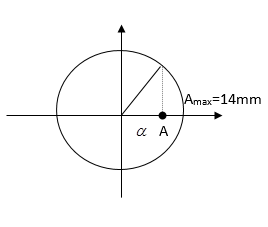
Cách 2: Hai nguồn cùng pha nên trung điểm I dao động cực đại:
Amax = 6 + 8 = 14mm
\(\cos \alpha = \dfrac{A}{{{A_{\max }}}} = \dfrac{{10}}{{14}} \to \alpha = 0,7751933733rad\)=$\varphi $
Độ lệch pha giữa I và M cần tìm là
\(\Delta \varphi = \dfrac{{2\pi }}{\lambda }d = 0,7751933733 \to d = 0,247cm\)
Hướng dẫn giải:
+ Cách 1: Viết phương trình sóng tại M và sử dụng điều kiện biên độ
+ Cách 2: Sử dụng vòng tròn lượng giác và công thức: \(\Delta \varphi = \dfrac{{2\pi }}{\lambda }d\)

