Một chất điểm dao động điều hoà thẳng trên trục $x'x$ xung quanh vị trí cân bằng $x = 0$ với chu kì dao động $T = 1,57s\left( { \approx \dfrac{\pi }{2}s} \right)$. Tại thời điểm $t = 0$ nó qua toạ độ ${x_0} = 25cm$ với vận tốc ${v_0} = 100cm/s$. Quãng đường vật đi được sau thời điểm $t = 0$ một thời gian $\dfrac{\pi }{8}s$ là :
Trả lời bởi giáo viên
Ta có: Tần số góc của dao động:
\(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{\frac{\pi }{2}}} = 4({\rm{r}}a{\rm{d}}/s)\)
- Tại t = 0: x0 = 25cm, v = 100 cm/s
Sử dụng hệ thức độc lập, ta có:
\({A^2} = {x^2} + {\left( {\frac{v}{\omega }} \right)^2} = {25^2} + {\left( {\frac{{100}}{4}} \right)^2} \to A = 25\sqrt 2 cm\)
Khoảng thời gian từ t = 0 đến một khoảng
\(\Delta t = \frac{\pi }{8}s = \frac{T}{4}\)
Quãng đường vật đi được sau thời điểm t = 0 một thời gian p/8 s là:
\(S = 2(A - \frac{A}{{\sqrt 2 }}) = 50\sqrt 2 - 50 = 20,711cm\)
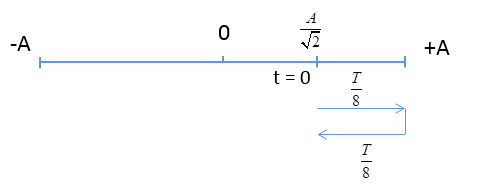
Hướng dẫn giải:
+ Áp dụng biểu thức xác định tần số góc của dao động: \(\omega = \frac{{2\pi }}{T}\)
+ Áp dụng hệ thức độc lập A - x - v:
\({A^2} = {x^2} + {\left( {\frac{v}{\omega }} \right)^2}\)
+ Sử dụng trục thời gian suy ra từ vòng tròn

