Câu hỏi:
2 năm trước
Đặt điện áp \(u = {U_0}{\rm{cos}}\omega {\rm{t}}\) (Uo và ω không đổi) vào hai đầu đoạn mạch AB theo thứ tự gồm một tụ điện, một cuộn cảm thuần và một điện trở thuần mắc nối tiếp. Gọi M là điểm nối giữa tụ điện và cuộn cảm. Biết điện áp hiệu dụng giữa hai đầu AM bằng điện áp hiệu dụng giữa hai đầu MB và cường độ dòng điện trong đoạn mạch lệch pha \(\dfrac{\pi }{{12}}\) so với điện áp giữa hai đầu đoạn mạch. Hệ số công suất của đoạn mạch MB là?
Trả lời bởi giáo viên
Đáp án đúng: d
Cách 1: Phương pháp đại số:
Do UAM = UMB => ZC = ZRL
Ta có:
\({\rm{cos}}\varphi {\rm{ = }}\dfrac{R}{{{Z_{MB}}}} = \dfrac{R}{{{Z_C}}}\)
\(\begin{array}{l}tan{\varphi _{AB}} = \tan \dfrac{\pi }{{12}} = \dfrac{{{Z_L} - {Z_C}}}{R} = \dfrac{{{Z_L}}}{R} - \dfrac{{{Z_C}}}{R} \\= \tan \varphi - \dfrac{1}{{{\rm{cos}}\varphi }} = \dfrac{{\sin \varphi - 1}}{{{\rm{cos}}\varphi }} \\= - \dfrac{{{\rm{cos}}\dfrac{\varphi }{2} - \sin \dfrac{\varphi }{2}}}{{{\rm{cos}}\dfrac{\varphi }{2} + \sin \dfrac{\varphi }{2}}}\\ \to \sin \dfrac{\varphi }{2}\left( {1 + \tan \dfrac{\pi }{{12}}} \right) = {\rm{cos}}\dfrac{\varphi }{2}\left( {1 - \tan \dfrac{\pi }{{12}}} \right) \\\to \tan \dfrac{\varphi }{2} = \dfrac{{\left( {1 - \tan \dfrac{\pi }{{12}}} \right)}}{{\left( {1 + \tan \dfrac{\pi }{{12}}} \right)}} = \dfrac{1}{{\sqrt 3 }} \\\to \dfrac{\varphi }{2} = {30^0} \\\to \varphi = {60^0}\\ \to c{\rm{os}}\varphi {\rm{ = 0}}{\rm{,5}}\end{array}\)
Cách 2: Sử dụng giản đồ véctơ
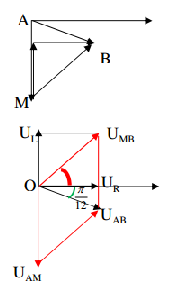
Ta có:
\(\angle O{U_{AB}}{U_{MB}} = \pi - \left( {\dfrac{\pi }{{12}} + \dfrac{\pi }{2}} \right) = \dfrac{{5\pi }}{{12}} = \angle {U_{MB}}O{U_{AB}}\) ( do tam giác OUMBUAB cân tại UMB )
\(\begin{array}{l} \to {\varphi _{MB}} = \angle {U_{MB}}O{U_R} = \dfrac{{5\pi }}{{12}} - \dfrac{\pi }{{12}} = \dfrac{\pi }{3}\\ \to c{\rm{os}}{\varphi _{MB}} = c{\rm{os}}\dfrac{\pi }{3} = 0,5\end{array}\)
Hướng dẫn giải:
Cách 1: Phương pháp đại số: sử dụng công thức \(\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R}\) và công thức hệ số công suất \({\rm{cos}}\varphi {\rm{ = }}\dfrac{R}{Z}\)
Cách 2: Sử dụng giản đồ véctơ
Câu hỏi khác
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
