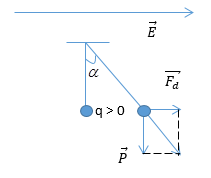
Một con lắc đơn gồm một quả cầu kim loại nhỏ, khối lương m = 1 g, tích điện dương q = 5,66.10-7 C, được treo vào một sợi dây mảnh dài ℓ = 1,4 m trong điện trường đều có phương ngang, E = 104 V/m, tại một nơi có gia tốc trọng trường g = 9,79 m/s2. Ở VTCB, phương của dây treo hợp với phương thẳng đứng một góc
Ta có:\(\overrightarrow E \) có phương ngang =>\(\overrightarrow {{F_d}} \) có phương ngang
Ta có:
\(\tan \alpha = \frac{{{F_d}}}{P} = \frac{{qE}}{{mg}} = \frac{{5,{{66.10}^{ - 7}}{{.10}^4}}}{{{{10}^{ - 3}}.9,79}} = 0,5781 \to \alpha = {30^0}\)
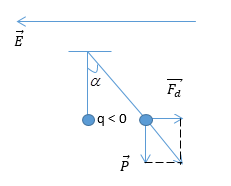
Con lắc đơn dài ℓ = 0,5 m, vật nặng có khối lượng m = 250 g mang điện tích q = - 5.10-5 C, cho g = 10 m/s2. Đặt con lắc vào vùng điện trường đều E có độ lớn E = 5.102 V/cm, có phương nằm ngang. Chu kì mới của con lắc là:
Ta có:
+ E = 5.102 V/cm = 5.104 V/m
+ \(\overrightarrow E \) có phương ngang =>\(\overrightarrow {{F_d}} \) có phương ngang
+ Chu kì dao động của con lắc tích điện q đặt trong điện trường đều là T’:
\(T' = 2\pi \sqrt {\frac{l}{{g'}}} \)
Ta có:
\(\begin{array}{l}a = \frac{{{F_d}}}{m} = \frac{{\left| q \right|E}}{m} = \frac{{\left| { - {{5.10}^{ - 5}}} \right|{{.5.10}^4}}}{{0,25}} = 10m/{s^2}\\g' = \sqrt {{g^2} + {a^2}} \\ \to T' = 2\pi \sqrt {\frac{l}{{g'}}} = 2\pi \sqrt {\frac{l}{{\sqrt {{g^2} + {a^2}} }}} = 2\pi \sqrt {\frac{1}{{\sqrt {{{10}^2} + {{10}^2}} }}} = 1,18{\rm{s}}\end{array}\)
Con lắc đơn trong phòng thí nghiệm có \(T = 2{\rm{ }}s\) được treo vào trần một ô tô. Cho \(g = {\pi}^2 m/s^2\) . Biết ôtô lên dốc nhanh dần đều với gia tốc \(a = \sqrt 3 g\). Biết dốc nghiêng một góc \(\beta {\rm{ }} = {\rm{ }}{30^0}\) so với phương ngang. Hãy xác định vị trí cân bằng của con lắc và chu kì dao động nhỏ của nó ?
Ta có:
+ Chu kì dao động của con lắc đơn khi ở trong phòng thí nghiệm: \(T = 2\pi \sqrt {\dfrac{l}{g}} \)
+ Oto lên nhanh dần trên dốc nghiêng (\(\overrightarrow a \) xiên lên) \( \to \overrightarrow {{F_{qt}}} \) xiên xuống
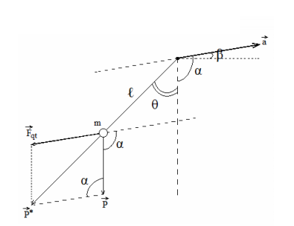
Ta có:
\(\begin{array}{l}P' = \sqrt {{P^2} + F_{qt}^2 - 2P{F_{qt}}{\rm{cos(90 + }}\beta {\rm{)}}} \\ \to g' = \sqrt {{g^2} + {a^2} - 2g.a.c{\rm{os(90 + }}\beta {\rm{)}}} = \sqrt {{g^2} + {a^2} - 2g.a.c{\rm{os(90 + 3}}{{\rm{0}}^0}{\rm{)}}} = 2,394g\\\dfrac{{T'}}{T} = \sqrt {\dfrac{g}{{g'}}} = \sqrt {\dfrac{g}{{2,394g}}} = 0,646 \to T' = 0,646.2 = 1,293{\rm{s}}\end{array}\)
Góc θ:
\(\dfrac{a}{{\sin \theta }} = \dfrac{{g'}}{{\sin ({{90}^0} + \beta )}} \to \sin \theta = \dfrac{{a\sin ({{90}^0} + \beta )}}{{g'}} = \dfrac{{\sqrt 3 g.\sin ({{90}^0} + 30)}}{{2,394g}} = 0,627 \to \alpha = {38^0}49'44\)
Con lắc đơn gồm một hòn bi có khối lượng m treo trên sợi dây dài ℓ = 1 m ở tại nơi có gia tốc trọng trường g = 9,8 m/s2. Bỏ qua mọi ma sát và lực cản môi trường. Con lắc trên được treo vào trần một ôtô chuyển động nhanh dần đều với gia tốc a = 2 m/s2 từ đỉnh mặt phẳng nghiêng với mặt phẳng ngang một góc 300. Hỏi con lắc dao động với chu kì bằng bao nhiêu ?
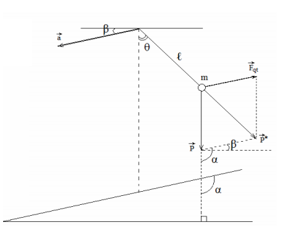
+ Oto lên nhanh dần xuống dốc nghiêng (\(\overrightarrow a \) xiên xuống) \( \to \overrightarrow {{F_{qt}}} \) xiên lên
Ta có:
\(\begin{array}{l}P' = \sqrt {{P^2} + F_{qt}^2 - 2P{F_{qt}}{\rm{cos(90 - }}\beta {\rm{)}}} \\ \to g' = \sqrt {{g^2} + {a^2} - 2g.a.c{\rm{os(90 - }}\beta {\rm{)}}} = \sqrt {{g^2} + {a^2} - 2g.a.c{\rm{os(90 - 3}}{{\rm{0}}^0}{\rm{)}}} = 8,969m/{s^2}\\ \to T' = 2\pi \sqrt {\frac{{\mathop{\rm l}\nolimits} }{{g'}}} = 2\pi \sqrt {\frac{1}{{8,969}}} = 2,098{\rm{s}}\end{array}\)
Một con lăc đơn có dây dài ℓ, vật nặng có \(m = 100 g\) tích điện \(q = + 5.10^{-6}C\) đặt trong điện trường điều cường độ E = 105 V/m và các đường sức hướng xiên góc β = 450 xuống dưới so với phương ngang. Bỏ qua mọi ma sát. Xác định vị trí cân bằng của con lắc và chiều dài dây treo con lắc. Biết chu kì dao động T = 2 s. Lấy g = 10 m/s2 và π2 = 10.
Ta có:
+ \(\overrightarrow E \) xiên xuống dưới, mà q > 0 => Lực điện trường \(\overrightarrow {{F_d}} \) xiên xuống dưới
Ta có:
\(\begin{array}{l}P' = \sqrt {{P^2} + F_d^2 - 2P{F_d}{\rm{cos(90 + }}\beta {\rm{)}}} \\ \to g' = \sqrt {{g^2} + {{\left( {\dfrac{{qE}}{m}} \right)}^2} - 2g.\left( {\dfrac{{qE}}{m}} \right).c{\rm{os(90 + }}\beta {\rm{)}}} = \sqrt {{{10}^2} + {{\left( {\dfrac{{{{5.10}^{ - 6}}{{.10}^5}}}{{0,1}}} \right)}^2} - 2g.\left( {\dfrac{{{{5.10}^{ - 6}}{{.10}^5}}}{{0,1}}} \right).c{\rm{os(90 + 45)}}} = 13,99m/{s^2}\\ \to T' = 2\pi \sqrt {\dfrac{l}{{g'}}} = 2{\rm{s}} \to l = \dfrac{{T{'^2}g'}}{{4{\pi ^2}}} = 1,399m\end{array}\)
Góc θ:
\(\dfrac{{\dfrac{{qE}}{m}}}{{\sin \theta }} = \dfrac{{g'}}{{\sin ({{90}^0} + \beta )}} \to \sin \theta = \dfrac{{\dfrac{{qE}}{m}\sin ({{90}^0} + \beta )}}{{g'}} = \dfrac{{5.\sin ({{90}^0} + 45)}}{{13,99}} = 0,253 \to \theta = {14^0}38'\)
Một học sinh dùng bộ thí nghiệm con lắc đơn để làm thí nghiệm đo độ lớn gia tốc trọng trường g tại phòng thí nghiệm Vật lí trường THPT Kim Liên. Học sinh chọn chiều dài con lắc là 55 cm, cho con lắc dao động với biên độ góc nhỏ hơn 100 và đếm được 10 dao động trong thời gian 14,925 s. Bỏ qua lực cản của không khí. Giá trị của g gần nhất với giá trị nào sau đây?
Chu kì của con lắc là:
\(T = \frac{t}{n} = \frac{{14,925}}{{10}} = 1,4925\,\,\left( s \right)\)
Lại có: \(T = 2\pi \sqrt {\frac{l}{g}} \)
\( \Rightarrow g = \frac{{4{\pi ^2}.l}}{{{T^2}}} = \frac{{4{\pi ^2}.0,55}}{{1,{{4925}^2}}} \approx 9,748\,\,\left( {m/{s^2}} \right)\)
Đề thi thử THPT chuyên Lam Sơn - 2021
Một con lắc đơn dao động điều hòa với chu kì T tại nơi có thêm ngoại lực có độ lớn F theo phương ngang. Nếu quay phương ngoại lực một góc \(\alpha \) \(\left( {{0^0} < \alpha < {{90}^0}} \right)\) trong mặt phẳng thẳng đứng và giữ nguyên độ lớn thì chu kì dao động là \({T_1} = 2,4{\rm{s}}\) hoặc \({T_2} = 4,8s\). Chu kì T gần giá trị nào nhất sau đây?
Con lắc đơn có chu kì dao động: \(T = 2\pi \sqrt {\frac{l}{g}} \)
\( \Rightarrow {T^2} = 4{\pi ^2}.\frac{l}{g} \Rightarrow g \sim \frac{1}{{{T^2}}}\)
+ Ban đầu \(\overrightarrow F \) theo phương ngang, ta có gia tốc biểu kiến khi này \(g' = \sqrt {{g^2} + {a^2}} \)
+ Khi \(\overrightarrow F \) hướng xuống
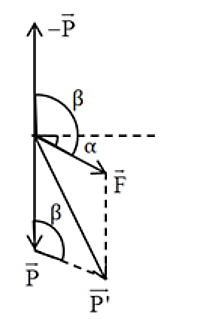
Có:\(\beta = {90^0} + \alpha \Rightarrow \cos \beta = \sin \alpha \)
Gia tốc hiệu dụng khi này: \({g_1} = \sqrt {{g^2} + {a^2} - 2ag\sin \alpha } \)
\( \Rightarrow g_1^2 = {g^2} + {a^2} - 2ag\sin \alpha \,\,\,\,\left( 1 \right)\)
+ Khi \(\overrightarrow F \) hướng lên trên
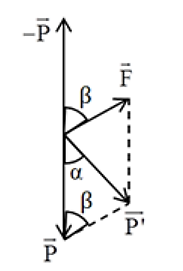
Ta có \(\beta = {90^0} - \alpha \Rightarrow co{\rm{s}}\beta = {\rm{ - sin}}\alpha \)
Gia tốc hiệu dụng khi này: \({g_2} = \sqrt {{g^2} + {a^2} + 2{\rm{a}}g\sin \alpha } \)
\( \Rightarrow g_2^2 = {g^2} + {a^2} + 2{\rm{a}}g\sin \alpha \,\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) ta có: \(g_1^2 + g_2^2 = 2\left( {{g^2} + {a^2}} \right)\)
\( \Rightarrow \frac{1}{{T_1^4}} + \frac{1}{{T_2^4}} = \frac{2}{{{T^4}}} \Leftrightarrow \frac{1}{{2,{4^4}}} + \frac{1}{{1,{8^4}}} = \frac{2}{{{T^4}}} \Rightarrow T = 1,9984{\rm{s}}\)

